The problem.
The 8-puzzle is a sliding puzzle that is played on a 3-by-3 grid with 8 square tiles labeled 1 through 8, plus a blank square. The goal is to rearrange the tiles so that they are in row-major order, using as few moves as possible. You are permitted to slide tiles either horizontally or vertically into the blank square. The following diagram shows a sequence of moves from an initial board (left) to the goal board (right).

Board data type.
To begin, create a data type that models an n-by-n board with sliding tiles. Implement an immutable data type Board .
Hamming and Manhattan distances. To measure how close a board is to the goal board, we define two notions of distance. The Hamming distance betweeen a board and the goal board is the number of tiles in the wrong position. The Manhattan distance between a board and the goal board is the sum of the Manhattan distances (sum of the vertical and horizontal distance) from the tiles to their goal positions.
Here keep care to make Board data-type immutable. So make sure not to make any changes in original board.. A catch for passing this assignment is to use a trick to save memory. As int[][] takes 24 + 32n + 4n^2 bytes of memory use a char[] array (of n*n length) for board and cast it to int (and vice versa) everytime. In order to locate position of 0 i have used an instance indexRow and indexColumn. (in order to find neighbors ) My board constructor is here:
public Board(int[][] tiles) {
n = tiles[0].length;
board = new char[n*n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
board[n*i+j] = (char)tiles[i][j];
if (board[n*i+j] == 0) {
indexRow = i;
indexColumn = j;
}
}
}
}

Hamming and Manhattan distances. To measure how close a board is to the goal board, we define two notions of distance. The Hamming distance betweeen a board and the goal board is the number of tiles in the wrong position. The Manhattan distance between a board and the goal board is the sum of the Manhattan distances (sum of the vertical and horizontal distance) from the tiles to their goal positions.
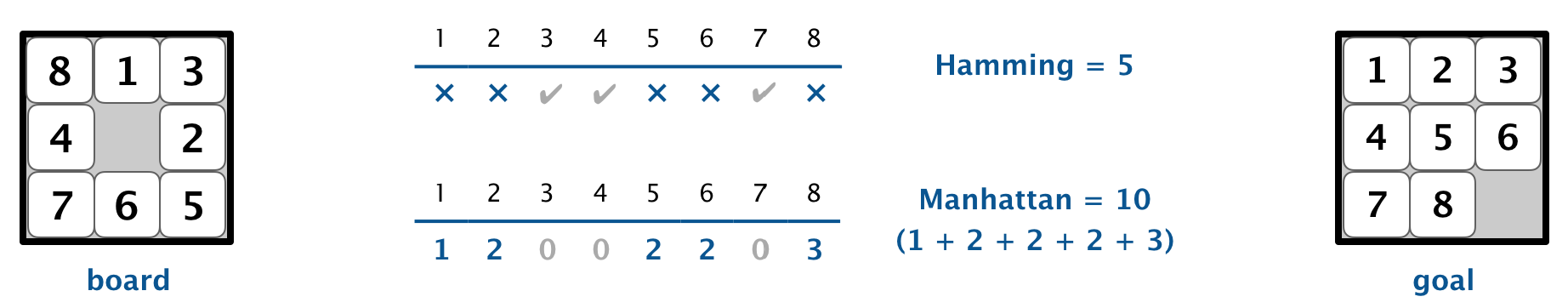
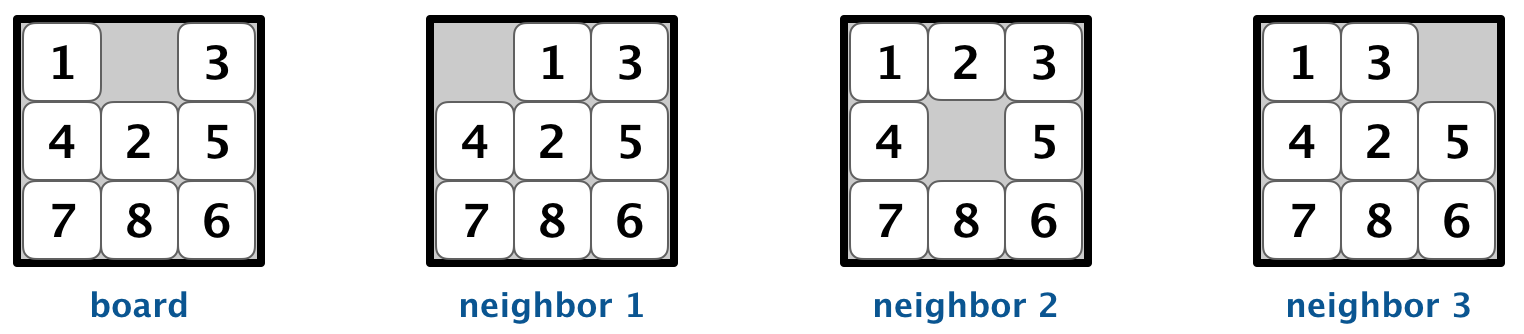
Solver data type.
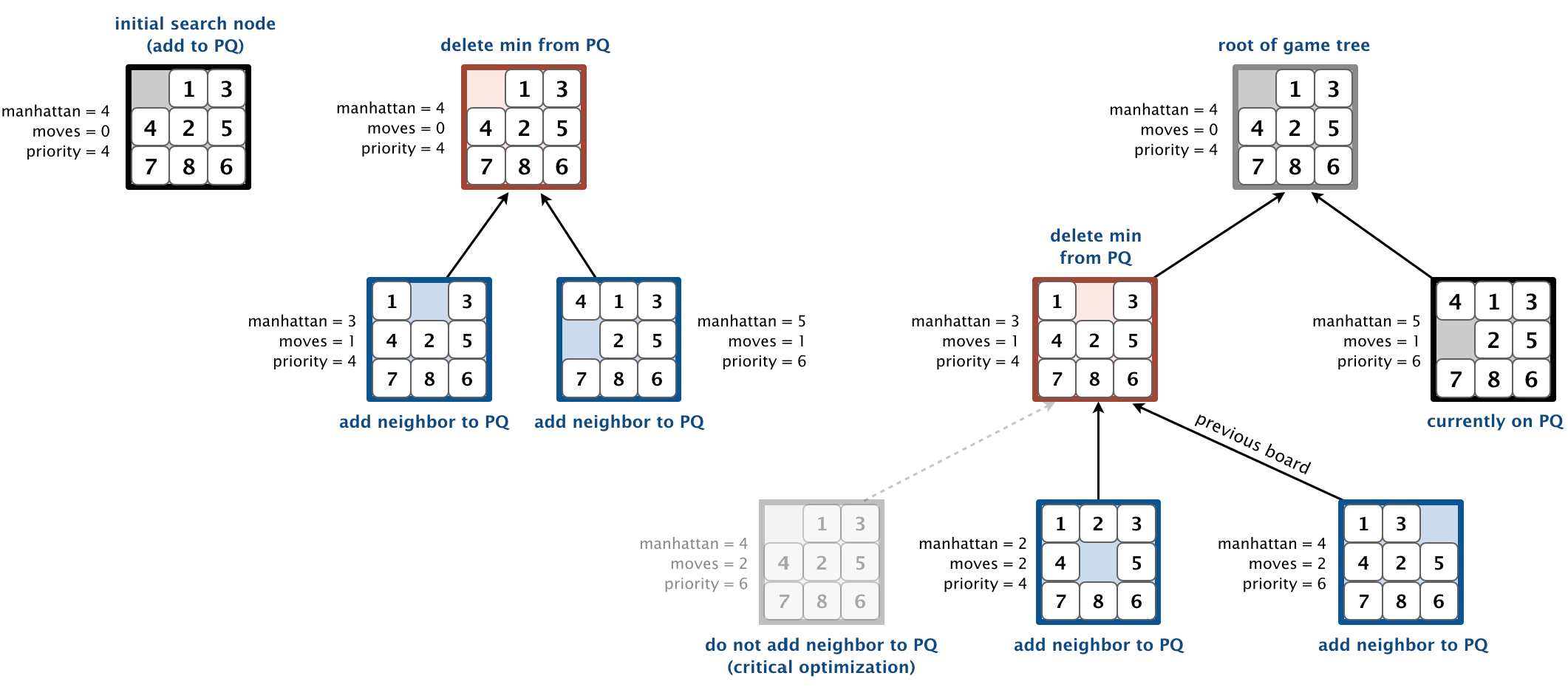
In this part, you will implement A* search to solve n-by-n slider puzzles. Create an immutable data type Solver with the following API:
Detecting unsolvable boards. Not all initial boards can lead to the goal board by a sequence of moves, including these two:
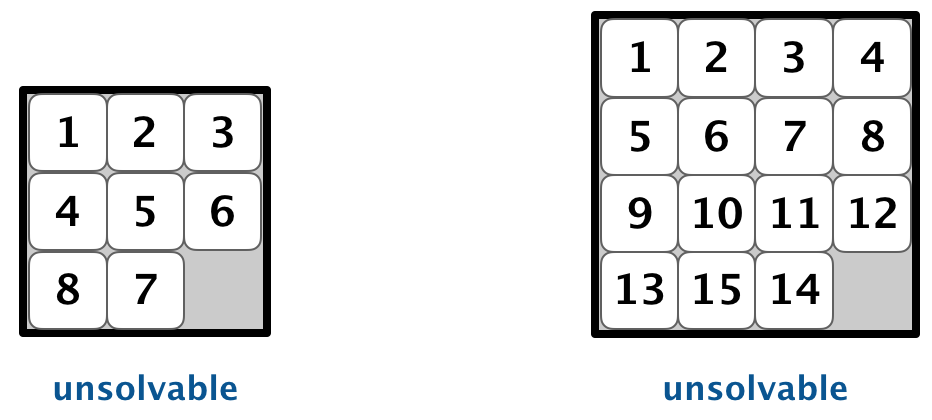
To detect such situations, use the fact that boards are divided into two equivalence classes with respect to reachability:
-
Those that can lead to the goal board
-
Those that can lead to the goal board if we modify the initial board by swapping any pair of tiles (the blank square is not a tile).
here in MinPq take two priority Queues: One to denote the board and another to denote a twin board. In order to save memory I have initialised two priority queues in constructor only so after that it doesnt occupy more space. whichever reaches goal board first breaks the loop and after that we can check if our board is solvable or not.
here is my pseudocode:
public Solver(Board initial) {
MinPQ<SearchNode> pq = new MinPQ<>();
MinPQ<SearchNode> pqI = new MinPQ<>();
curr= new SearchNode(initial, null);
SearchNode twin=new SearchNode(initial.twin(), null);
pq.insert(curr);
pqI.insert(twin);
while (!curr.board.isGoal() && !twin.board.isGoal()) {
curr = pq.delMin();
twin = pqI.delMin();
for (Board nb : curr.board.neighbors()) {
if (curr.previousNode == null || !nb.equals(curr.previousNode.board))
{ pq.insert(new SearchNode(nb, curr));}
}
for (Board nb : twin.board.neighbors()) {
if (twin.previousNode == null || !nb.equals(twin.previousNode.board))
pqI.insert(new SearchNode(nb, twin));
}
}
if (curr.board.isGoal()) {
solvable = true;
}
}
Test client.
The following test client takes the name of an input file as a command-line argument and prints the minimum number of moves to solve the puzzle and a corresponding solution.
public class Client {
public static void main(String[] args) {
// create initial board from file
In in = new In(args[0]);
int n = in.readInt();
int[][] tiles = new int[n][n];
for (int i = 0; i < n; i++)
for (int j = 0;j < n; j++)
tiles[i][j] = in.readInt();
Board initial = new Board(tiles);
// solve the puzzle
Solver solver = new Solver(initial);
// print solution to standard output
if (!solver.isSolvable())
StdOut.println("No solution possible");
else {
StdOut.println("Minimum number of moves = " + solver.moves());
for (Board board : solver.solution()){
// System.out.println("board called");
StdOut.println(board);}
}
}
}